그래프를 탐색하는 방법으로 DFS와 BFS가 많이 언급된다. 실제로 코딩 테스트 문제로 자주 출제되며, 경험상 해당 문제들을 이러한 알고리즘 기법 도구들을 사용하지 않고 다가가면 아주 어려웠다. 그러나 DFS와 BFS라는 도구를 익힌다면 엄청 어려워 보이던 최단 거리 구하기 같은 문제들에 자신감이 생기게 된다. 알기 전과 후의 차이가 극명한 알고리즘으로 이번 기회에 정리를 해두면 도움이 될 것 같다.
(엘리스 sw트랙 스터디 활동으로 [이것이 취업을 위한 코딩 테스트]다의 DFS 및 BFS 강의를 기반으로 작성한다.)
깊이 우선 탐색 (DFS : Depth First Search)
우선 DFS라고 불리는 깊이 우선 탐색을 먼저 살펴본다. 트리나 그래프 구조에서 각 노드를 검사하는 방법으로 다음 branch로 넘어가기 전 해당 branch를 완전히 탐색하는 방식으로 진행된다. 말 그대로 깊이 우선 탐색이다. 그렇다면 어떻게 이것을 적용할 수 있을까?
How?
DFS를 코드로 구현하기 위해서 우선 stack 혹은 재귀함수가 사용된다. 스택은 선입후출(FILO) 형식의 자료 구조이며 노드 방문 상태를 저장해두기 위해서 사용한다. 알고리즘의 자세한 동작 과정은 다음과 같다.
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 더 이상 2번 과정을 수행할 수 없을 때까지 반복한다.
When?
1. 모든 노드를 방문하여 확인해야할 때
2. 길 찾기 (미로 찾기)
3. 순회
특징
- 단순 검색 속도가 BFS보다 느리다
- 리프 노드에만 데이터를 저장하는 정렬 트리 구조에서 항상 순서대로 데이터를 방문한다
- 노드 방문 시 반드시 해당 노드 방문 여부를 검사해야 무한 루프에 빠지는 것을 피할 수 있다
DFS 소스 코드 참고
# DFS 메서드 정의 (이코테)
def dfs(graph, v, visited):
visited[v] = True # 현재 노드를 방문 처리
#현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
# 각 노드가 방문된 정보 표현 (1차원 list)
visited = [False] * 9
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)너비 우선 탐색 (BFS : Breadth-First Search)
바늘 가는 곳에 실이 가듯 DFS가 있는 곳에는 BFS도 함께 비교된다. DFS와는 다르게 너비를 우선적으로 탐색하는 방법이다. 가까운 노드부터 우선적으로 탐색하므로 주로 최단 거리를 구하는 문제에 사용할 수 있다.
How?
스택을 사용하던 DFS와는 다르게 BFS에서는 큐 자료구조가 사용된다. 큐는 먼저 들어 온 데이터가 먼저 나가는 형식인 선입선출(FIFO) 방식의 자료구조이다. 가까운 노드를 우선적으로 처리해야하기 때문에 큐 자료구조가 적격이다. 자세한 동작은 아래와 같다.
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
When?
1. 두 노드 사이의 최단 거리를 찾을 때
2. 최소 비용을 찾을 때
특징
- 경로가 길어질수록 탐색 branch의 급격한 증가로 인한 많은 메모리 필요
- 간선에 가중치가 동일할 때(가중치가 없을때) 최단 경로를 보장한다
동작 예시 확인하기
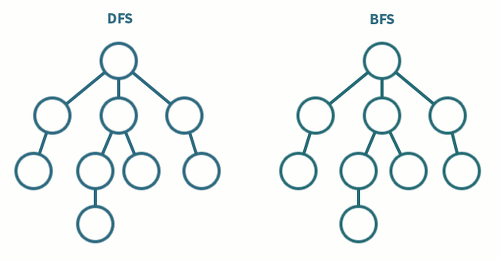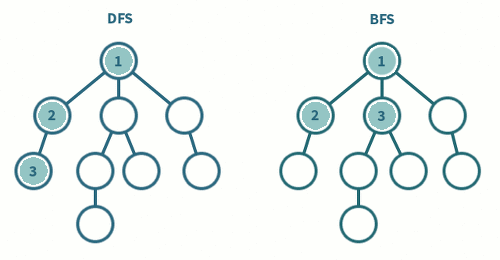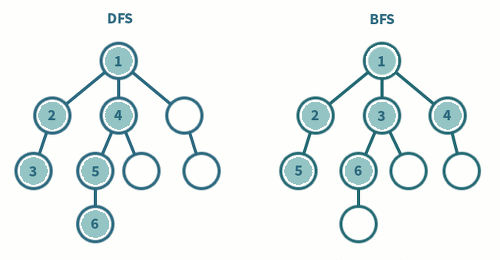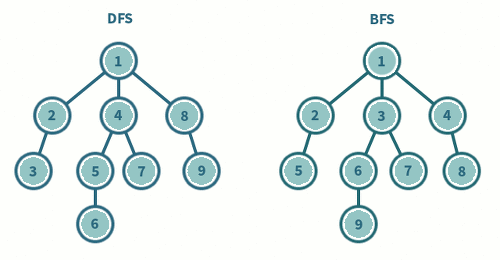
같은 그래프를 준비하고 DFS와 BFS를 각각 파이썬 코드로 구현해보자. 우선 그래프는 다음 그림과 같다.
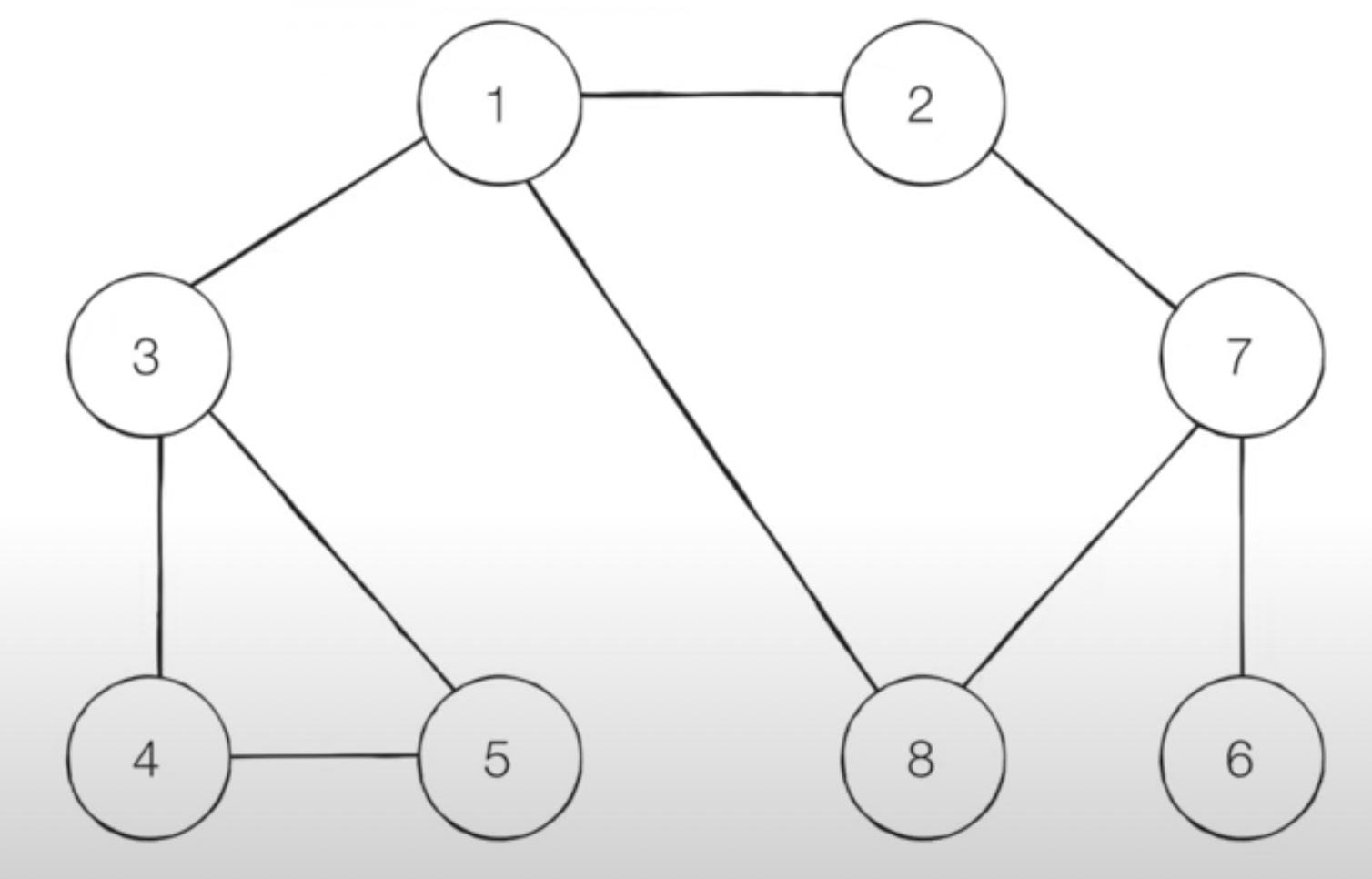
주어진 노드들의 그래프를 코드로 표현해보자. 각 노드마다의 간선으로 연결된 다른 노드들에 대한 정보를 어떻게 코드로 구현할까? 그 방법은 2차원 리스트를 이용하는 것이 일반적이다. 예를 들어 1번 노드의 인접 노드를 리스트로 나타낸다면 [2, 3]이다. 또한 7번 노드의 인접 노드를 리스트로 [2, 6, 8]과 같이 나타낼 수 있다. 이를 통해 graph의 할당은 다음과 같이 할 수 있다.
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
1에서 시작한다고 가정할 때 DFS 방식의 탐색 순서는 1 - 2 - 7 - 6 - 8 - 3 - 4 - 5 의 순서로 진행된다. 인접한 노드가 두개 이상일 때에는 번호가 낮은 노드를 우선적으로 방문한다. 이를 파이썬 코드로 구현하면
# DFS 메서드 정의 (이코테)
def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end=" ")
#현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
# 각 노드가 방문된 정보 표현 (1차원 list)
visited = [False] * 9
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)
반면 같은 그래프를 두고 BFS 방식으로 탐색을 한다면 1 - 2 - 3 - 8 - 7 - 4 - 5 - 6 의 순서로 각 노드들을 방문할 것이다. 마찬가지로 낮은 번호의 노드를 우선적으로 탐색하였다. BFS에 대한 코드도 살펴보자.
from collections import deque
# BFS 메서드 정의
def bfs(graph, start, visited):
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque([start])
# 현재 노드 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
v = queue.popleft() # 큐에서 하나의 원소를 뽑아 출력
# 아직 방문하지 않은 인접한 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visitied[i] = True
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
# 각 노드가 방문된 정보 표현
visited = [False] * 9
# 정의된 BFS 함수 호출
bfs(graph, 1, visited)결론
솔직히 이 글을 쓰면서 많이 답답했다. 차례대로 각 노드를 탐색하며 발생되는 과정을 GIF 파일로 보기 좋게 그리고 싶었다. 알고리즘의 이해에 대한 문제가 아니라, 머릿속에서 상상되는 그림을 표현하기 힘든게 문제였다. 그렇다고 애프터이펙트를 구독하고 공부하는 것에 투자를 하기에도 애매하다. 움직이는 도형을 표현할 방법을 좀 더 찾아봐야겠다. 그럼 아쉬운 마음에 가장 간결하고 직관적으로 알고리즘을 떠올릴 수 있는 GIF를 올린다.
어쨌든 DFS와 BFS는 자료구조 Stack과 Queue를 사용할 줄 알면서 각각의 매커니즘을 이해했다면 사용하는데에 무리가 없을 것으로 보인다. 코딩 테스트에 임할 때에는 물론 문제 해석을 통한 그래프 떠올리기, 그래프를 2차원 배열로 변환하기 그리고 구현하기 등 추가적으로 필요한 역량이 필수적이다. 이제 관련 문제들을 풀어봐야겠다.
참조
'코딩 테스트 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 구현 알고리즘 - 시뮬레이션 및 완전 탐색 (0) | 2022.09.28 |
|---|---|
| [알고리즘] 그리디 알고리즘(탐욕법) (1) | 2022.09.28 |

